How an amateur mathematician can ruin a quiz
On Facebook a friend of mine posted the image below, and many people, including myself, posted answers. It is a nice problem in that it requires one to look very closely at the details to get an answer. This problem, it seems to me, has some very subtle ideas in it, and I would like to share my thoughts about them here. If you would like to solve this problem for yourself, you should do it now as I am apt to give away some of the possible answers below.
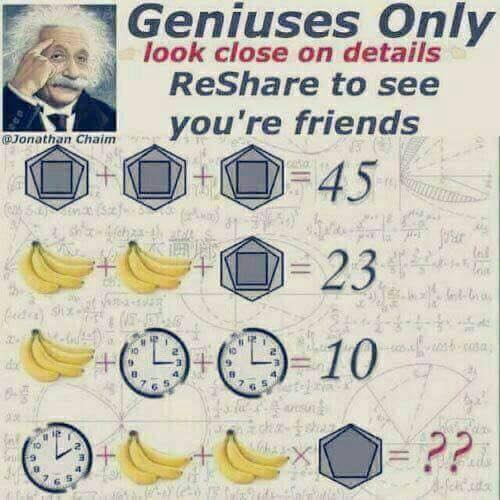
First we are give three equations with 3 unknowns. The unknowns being: 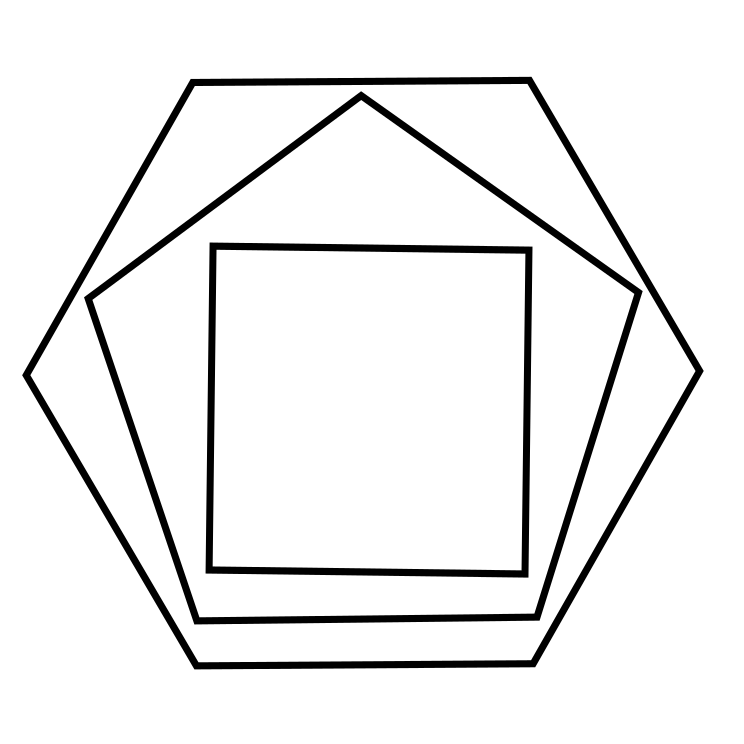 ,
,  , and
, and  .
.
 +
+  +
+  = 45
= 45 +
+  +
+  = 23
= 23 +
+  +
+  = 10
= 10
There are several way to solve this. One of the more fun would be to use Gaussian elimination or you can use one of the many other ways to solve a system of linear equations.
To save some space and typing I am going to give the images above names. Let us refer to the image  as g3.15 as there are 3 geometrical shapes with 15 sides. Let us refer to the image
as g3.15 as there are 3 geometrical shapes with 15 sides. Let us refer to the image  as b4 as there are 4 bananas. let us refer to the image
as b4 as there are 4 bananas. let us refer to the image  as c3 as the hour hand is on the 3.
as c3 as the hour hand is on the 3.
So now we can rewrite the equations above as:
3·g3.15 = 45, or 45/3 = 15 = g3.15
2·b4 + 15 = 23 or (23 - 15) / 2 = 4 = b4
2·c2 + 4 = 10 or (10 - 4) / 2 = 3 = c3
So we have g3.15 ( ) = 15 ,b4 (
) = 15 ,b4 ( ) = 4 , and c3 (
) = 4 , and c3 ( ) = 3
) = 3
And now we come to the interesting part. Where we try to come up with a solution. There are 2 (or is it 4) tricks here. The first is that multiplication was added· and the images have slightly changed.
 +
+  +
+  ×
×  = ??
= ??I will name the new images
 as c2 as the hour hand is now on the 2,
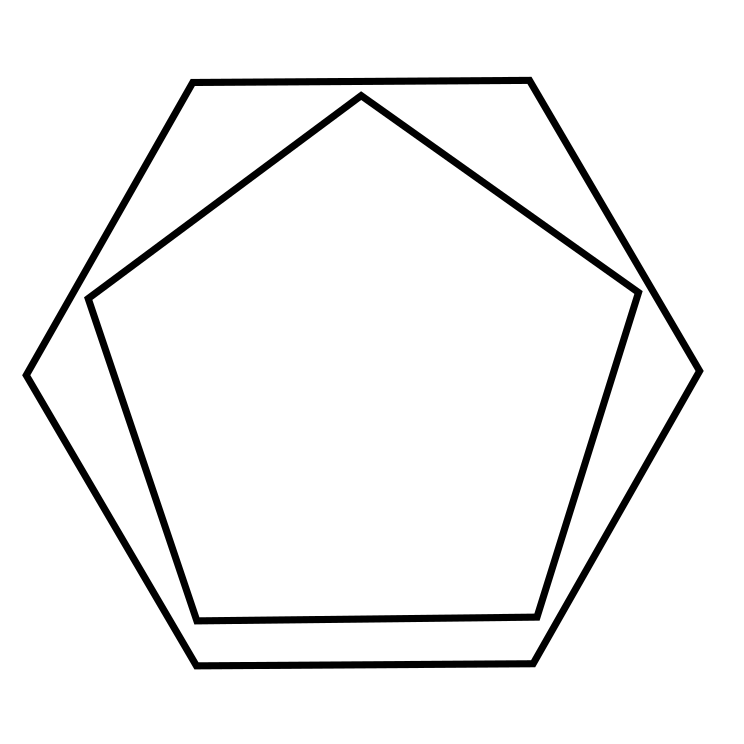
as c2 as the hour hand is now on the 2,  as g2.11 as there are 2 geometrical shapes with 11 sides and,
as g2.11 as there are 2 geometrical shapes with 11 sides and,  as b3 as there are now only 3 bananas.
as b3 as there are now only 3 bananas.So what is the answer? Well my friend is of the opinion that the answer is 38, and this is certainly a reasonable answer. But how did we get to this answer?
Well (most of us) surmised that if a clock with the hour hand on 3 has a value of 3 and a bunch of 4 bananas has and value of 4 and polygons with 15 sides have a value of 15, then it is reasonable to assume that a clock with the hour hand on 2 will have a value of 2, and a bunch of 3 bananas will have a value of three and polygons with 11 sides will have a value of 11. From this we then get the equation c2 + b3 + b3 · g2.11 = 2 + 3 + 3 · 11 = 2 + 3 + 33 = 38.
What we have done here is created 3 functions:
- a function that maps clocks (or images of clocks) to a subset of the real numbers. We will call it fclock.
- a function that maps banana bunches (or images of banana bunches) to a subset of the real numbers. We will call it fbanana.
- a function that maps polygons (or images of polygons) to a subset of the real numbers. We will call it fpolygons.
To come up with the answer 38 we used these functions:
fclock(i) = i:hour
fbanana(i) = i:count
fpolygons(i) = i:sides
And with those functions you get the answers:
fclock( ) = 3
) = 3
fclock( ) = 2
) = 2
fbanana( ) = 4
) = 4
fbanana( ) = 3
) = 3
fpolygons( ) = 15
) = 15
fpolygons( ) = 11
) = 11
But (rather obviously) the polygon images have more information than just the number of sides, they also has the number of polygons.
What if we change the function fpolygons to fpolygons(i) = i:polygons * i:sides / 3
 ) is still equal to 15 (3/3 · 15) but now fpolygons(
) is still equal to 15 (3/3 · 15) but now fpolygons( ) will be equal to 2 · 11 / 3 or 7 1/3
) will be equal to 2 · 11 / 3 or 7 1/3Now the answer to the problem is 2 + 3 + 3 · 7 1/3 = 5 + 22 = 27
So 27 is certainly as good an answer as 38.
So what are the answers to the problem - well it is any number you want. I have limited my functions to real numbers, but there is no reason that they could not output interesting numbers. Here is a set of functions that will give us the answer PI.
fclock(i) = i:hour·(3 - π) + 3· π - 6
fbanana(i) = 4 · i:count - 12
fpolygons(i) = i:sides
First lest make sure our functions put out the correct values:
- fbanana(
 ) = 4 · 4 - 12 = 4
) = 4 · 4 - 12 = 4 -
fpolygons(
 ) is obviously equal to 15.
) is obviously equal to 15.
-
fclock(
 ) = 3 · (3 - π) + 3 · π - 6 = 3
) = 3 · (3 - π) + 3 · π - 6 = 3
- fbanana(
 ) = 4 · 3 - 12 = 0
) = 4 · 3 - 12 = 0 -
fpolygons(
 ) = 11
) = 11
-
fclock(
 ) = 2 · (3 - π) + 3 · π - 6 = π
) = 2 · (3 - π) + 3 · π - 6 = π
 ) +
fbanana(
) +
fbanana( ) +
fbanana(
) +
fbanana( ) ·
fpolygons(
) ·
fpolygons( )
= (2 · (3 - π) + 3 · π - 6) + 0 + 0 · 11 = π
)
= (2 · (3 - π) + 3 · π - 6) + 0 + 0 · 11 = π
fbanana(
 ) = 4 · 4 - 12 = 4
Since fbanana(
) = 4 · 4 - 12 = 4
Since fbanana( ) is zero we can ignore
and then fclock(
) is zero we can ignore
and then fclock( ) = 2 · (3 - π) + 3 · π - 6 = π
) = 2 · (3 - π) + 3 · π - 6 = π